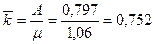Реферат: Контрольная работа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Томский государственный университет систем управления
и радиоэлектроники (ТУСУР)
Кафедра Экономики
Контрольная работа
по дисциплине “Математические модели в Экономике ”
Вариант №18
Выполнил:
Студент гр. з822
________ Васенин П.К.
Проверила:
________ Сидоренко М.Г.
г. Томск 2003
Задание №1
1. Объём
выпуска продукции Y зависит от количества вложенного
труда x как функция
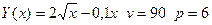 .
Цена продукции v, зарплата p.
Другие издержки не учитываются. Найти оптимальное количество вложенного труда.
.
Цена продукции v, зарплата p.
Другие издержки не учитываются. Найти оптимальное количество вложенного труда.
Решение:
Оптимальное количество вложенного
труда обозначим через X*
Определим прибыль 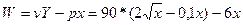
Воспользуемся соотношением 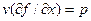 - т.е. частные производные
приравняем к нулю, найдём оптимальное количество вложенного труда
- т.е. частные производные
приравняем к нулю, найдём оптимальное количество вложенного труда
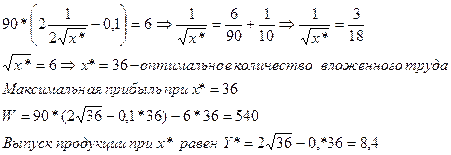
Задание №2
2. Даны
зависимости спроса D=200-2p и
предложения S=100+3p от цены.
Найдите равновесную
цену, цену при которой выручка
максимальна и эту максимальную выручку.
Решение:
Равновесная цена находится путём
приравиевания спроса и предложения, т.е. 200-2p=100+3p; p*=20 – равновесная цена.
Найдём прибыль при равновесной
цене:
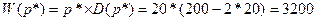
Найдём цену, определяющую
максимум выручки:
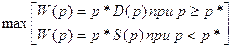
При p*(200-2p) максимум достигается в точке p’=50
(определили через производную)
W
(50)=50*(200-2*50)=5000
Таким образом, максимальная
выручка W(p’)=5000 достигается
не при равновесной цене.
Задание №3
3. Найти
решение матричной игры (оптимальные стратегии и цену игры) 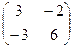 .
.
Решение:
1- способ. Проверим на
наличие седловой точки. Седловая точка является одновременно наименьшим
элементом строки и наибольшим элементом столбца. В матрице седловой точки нет.
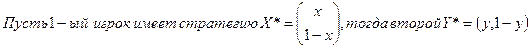 Выигрыш
первого есть случайная величина с рядом распределения:
Выигрыш
первого есть случайная величина с рядом распределения:
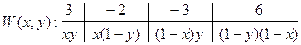
Найдём средний выигрыш за партию
Первого – это математическое ожидание случайной величины W(x,y):
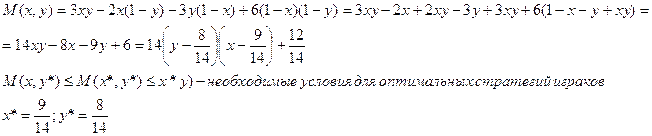
Оптимальные стратегии игроков:
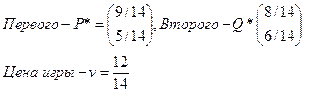
2 – способ. Если решить
эту игру как матричные игры двух игроков с нулевой суммой, то для игры с
матрицей 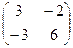 оптимальные смешанные для 1
и 2 игроков и цена игры получаются из решения уравнений:
оптимальные смешанные для 1
и 2 игроков и цена игры получаются из решения уравнений:
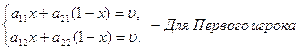
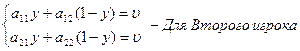
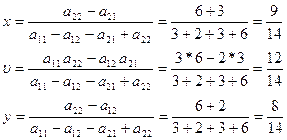
Откуда, Оптимальные стратегии
игроков:
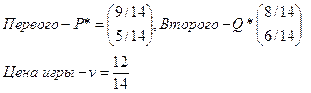
Задание №4
4. Для
трехотраслевой экономической системы заданы матрица коэффициентов прямых
материальных затрат 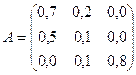 и вектор конечной
продукции
и вектор конечной
продукции 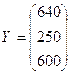 . Найти коэффициенты полных
материальных затрат двумя способами (с помощью формул обращения невыраженных
матриц и приближённо), заполнить схему межотраслевого баланса.
. Найти коэффициенты полных
материальных затрат двумя способами (с помощью формул обращения невыраженных
матриц и приближённо), заполнить схему межотраслевого баланса.
Решение:
I.
Определим матрицу коэффициентов полных материальных затрат приближённо,
учитывая косвенные затраты до 2-го порядка включительно.
Матрица косвенных затрат первого
порядка:
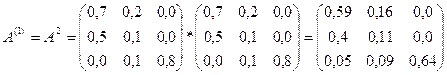
Матрица косвенных затрат второго
порядка:
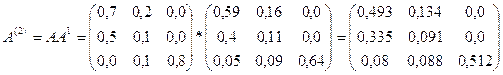
Получаем матрицу коэффициентов
полных материальных затрат (приближённо):
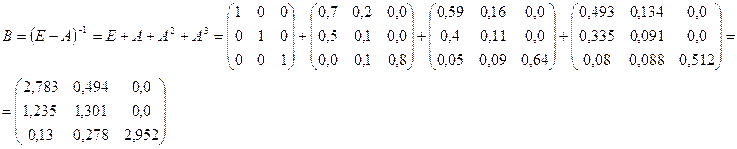
II.
Определим матрицу коэффициентов полных материальных затрат с помощью
формул обращения невыраженных матриц:
a) Находим
матрицу (E-A):
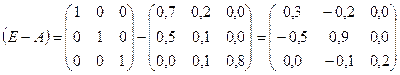
b) Вычисляем
определитель этой матрицы:
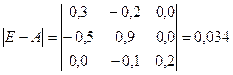
c) Транспонируем
матрицу (E-A):
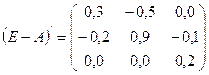
d) Находим
алгебраические дополнение для элемента матрицы (E-A)’:
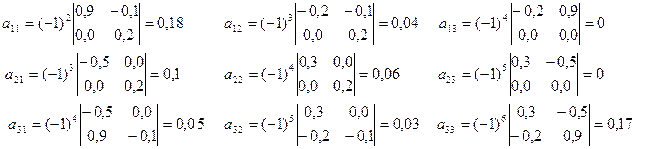
Таким образом:
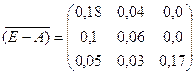
e) Находим
матрицу коэффициентов полных материальных затрат:
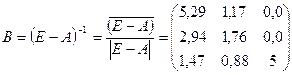
Таким образом,
расчёты первым и вторым способом получились разные – это произошло из-за того,
что второй способ наиболее точен (рассчитан по точным формулам), а первый
способ рассчитан приближённо, без учёта косвенных затрат выше второго порядка.
Для заполнения
межотраслевого баланса необходимо найти величину валовой продукции:
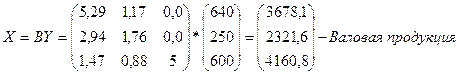
Схема межотраслевого баланса
|
Производящие
отрасли
|
Потребляющие
отрасли
|
|
1
|
2
|
3
|
Конечная
продукция
|
Валовая
продукция
|
|
1
2
3
|
2574,67
1839,05
0
|
464,32
232,16
232,16
|
0
0
3328,64
|
640
250
600
|
3678,1
2321,6
4160,8
|
|
Условно чистая
продукция
|
-735,62
|
1392,96
|
832,16
|
1490
|
|
|
Валовая
продукция
|
3678,1
|
2321,6
|
4160,8
|
|
10160,5
|
Задание №5
5. Проверить
ряд 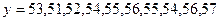 на наличие выбросов методом
Ирвина, сгладить методом простой скользящеё средней с интервалом сглаживания 3,
методом экспоненциального сглаживания (а=0,1), представить результаты
графически, определить для ряда трендовую модель в виде полинома первой степени
(линейную модель), дайте точечный и интервальный прогноз на три шага вперёд.
на наличие выбросов методом
Ирвина, сгладить методом простой скользящеё средней с интервалом сглаживания 3,
методом экспоненциального сглаживания (а=0,1), представить результаты
графически, определить для ряда трендовую модель в виде полинома первой степени
(линейную модель), дайте точечный и интервальный прогноз на три шага вперёд.
Решение:
a)
Проверим ряд на наличие выбросов методом Ирвина. Метод Ирвина Служит для
выявления аномальных уровней, т.е. – это отдельное значение временного ряда
которое не отвечает потенциальным возможностям исследуемой экономической
системы и которое, оставаясь в качестве значения уровня ряда, оказывает
существенное влияние на значение основных характеристик временного ряда, и на
трендовую модель.
Для выявления
аномальных уровней воспользуемся формулой:
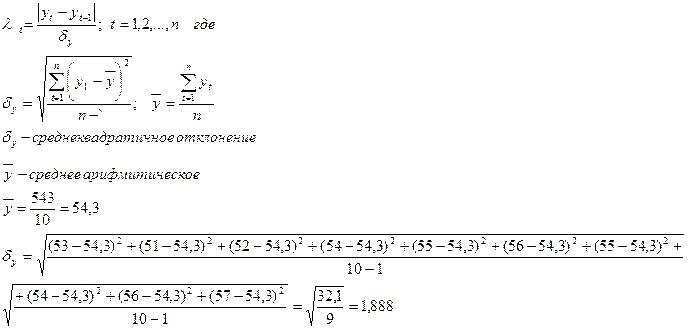
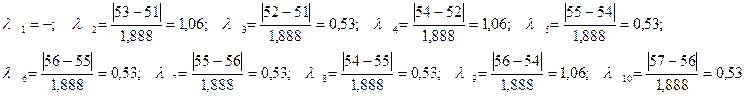 Расчётные значения:
Расчётные значения:
| t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
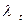
|
- |
1,06 |
0,53 |
1,06 |
0,53 |
0,53 |
0,53 |
0,53 |
1,06 |
0,53 |
Необходимо, расчётные значения
сравнить с табличными критерия Ирвина 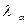 ,
и если окажется, что расчётное больше табличного, то соответствующее значение
,
и если окажется, что расчётное больше табличного, то соответствующее значение 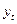 уровня ряда считается
аномальным.
уровня ряда считается
аномальным.
Табличные значения для уровня значимости a=0,05, т.е. с 5% ошибкой:
| n |
2 |
3 |
10 |
20 |
30 |
50 |
100 |
|
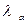
|
2,8 |
2,3 |
1,5 |
1,3 |
1,2 |
1,1 |
1 |
Таким образом, при сравнении
значений, обнаруживаем, что аномальных уровней нет, т.е.  .
.
b)
Сгладим методом простой скользящей средней с интервалом сглаживания m=3:
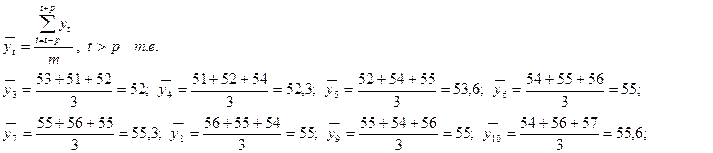
| t |
|
Метод простой
скользящей средней, 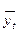
|
| 1 |
53 |
-- |
| 2 |
51 |
-- |
| 3 |
52 |
52 |
| 4 |
54 |
52,3 |
| 5 |
55 |
53,6 |
| 6 |
56 |
55 |
| 7 |
55 |
55,3 |
| 8 |
54 |
55 |
| 9 |
56 |
55 |
| 10 |
57 |
55,6 |
c)
Сгладим экспоненциальным методом с а=0,1 – параметр сглаживания:
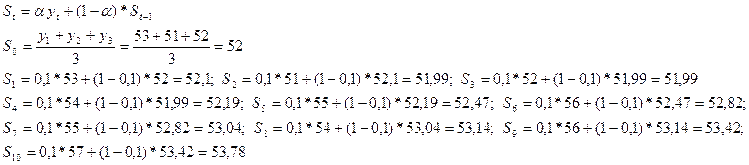
| t |
|
Экспоненциальный
метод, 
|
| 1 |
53 |
52,1 |
| 2 |
51 |
51,99 |
| 3 |
52 |
51,99 |
| 4 |
54 |
52,19 |
| 5 |
55 |
52,47 |
| 6 |
56 |
52,82 |
| 7 |
55 |
53,04 |
| 8 |
54 |
53,14 |
| 9 |
56 |
53,42 |
| 10 |
57 |
53,78 |
d) Представим
результаты графически:
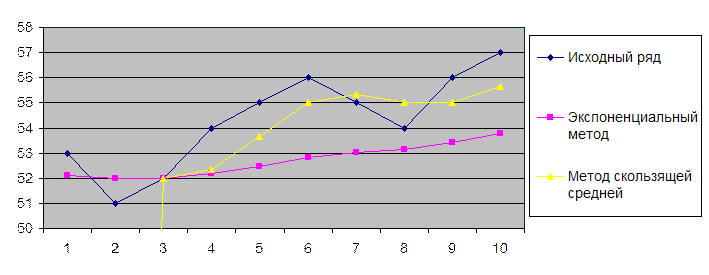
e)
Определим для ряда трендовую модель в виде полинома первой степени
(линейную модель):
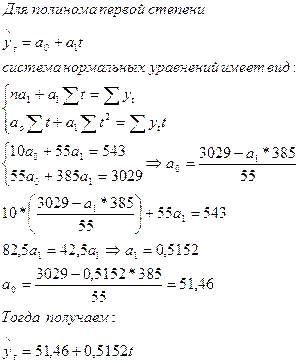
Необходимо оценить адекватность и точность построения модели, т.е.
необходимо выполнение следующих условий:
a)
Проверка случайности колебаний уровней остаточной последовательности:
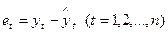
Проверку
случайности уровней ряда проведем по критерию пиков, должно выполняться: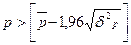
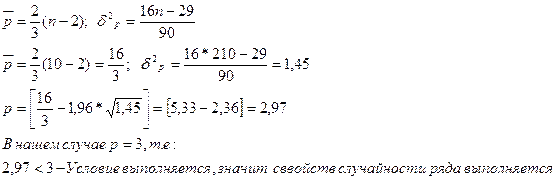
| t |
Фактическое 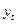
|
Расчётное 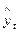
|
Отклонение 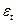
|
Точки пиков |
|
1
2
3
4
5
6
7
8
9
10
|
53
51
52
54
55
56
55
54
56
57
|
51,97
52,49
53
53,52
54,03
54,55
55,06
55,58
56,09
56,61
|
1,03
-1,49
-1
0,48
0,97
1,45
-0,06
-1,58
-0,09
0,39
|
--
1
0
0
0
1
0
1
0
--
|
| 55 |
543 |
542,9 |
0,1 |
3 |
b)
Проверка соответствия распределения случайной компоненты нормальному
закону распределения:
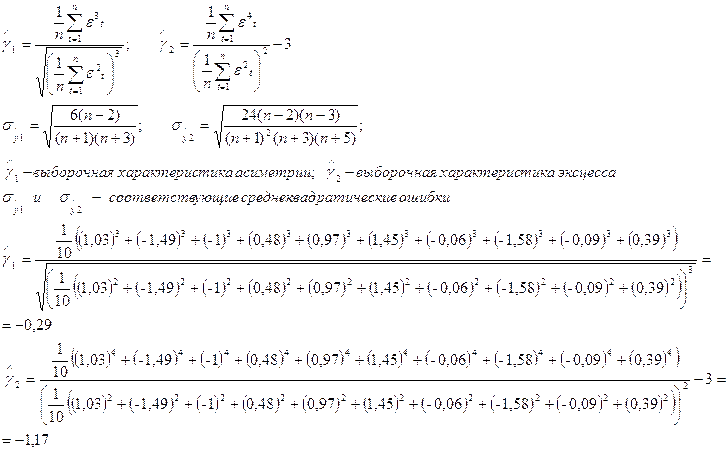
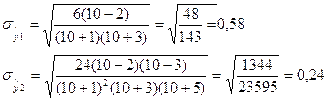
Необходимые
условия:
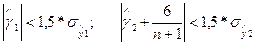
Если эти условия выполняются одновременно, то гипотеза о характере
распределения случайной компоненты принимается, если выполняется хотя бы одно
из следующих неравенств:
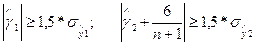
то гипотеза о нормальном
распределении отвергается, трендовая модель признаётся неадекватной.
1)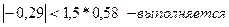
2)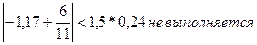
Таким образом,
одно из неравенств не выполняется, трендовая модель неадекватна, значит,
дальнейшее исследование не имеет смысла.
Задание №6
6. Пункт
по приёму квартир работает в режиме отказа и состоит из двух бригад.
Интенсивность потока 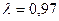 ,
производительность пункта
,
производительность пункта 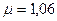 .
Определить вероятность того, что оба канала свободны, один канал занят, оба
канала заняты, вероятность отказа, относительную и абсолютную пропускную
способности, среднее число занятых бригад.
.
Определить вероятность того, что оба канала свободны, один канал занят, оба
канала заняты, вероятность отказа, относительную и абсолютную пропускную
способности, среднее число занятых бригад.
Решение:
Коэффициент использования
(количество заявок, поступающих за время использования одной заявки)
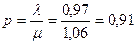
a)
Вероятность того, что оба канала свободны:
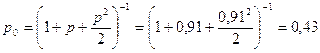
b)
Вероятность того, что один канала занят:
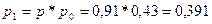
c)
Вероятность того, что оба канала заняты:
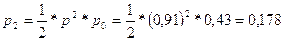
d) Вероятность
отказа в заявке:
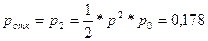
e)
Относительная пропускная способность:
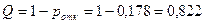
f)
Абсолютная пропускная способность:
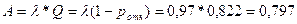
g)
Среднее число занятых бригад: