Реферат: Рекурсия

.

С понятием рекурсии мы уже встречались: рекуррентные соотношения довольно часто встречаются в математических выражениях. Рекурсия в определении состоит в том, что определяемое понятие определяется через само это понятие. Примером здесь может служить определение высказывания (см. лекция 5, определение 5.1). Рекурсия в вычислениях выступает в форме рекуррентных соотношений, которые показывают, как вычислить очередное значение, используя предыдущие.

   Например, рекуррентное соотношение

xi=xi-2+xi-1  ,   где  x1=1 , x2=2

задает правило вычисления так называемых чисел Фибоначчи.

   Другим примером рекуррентных соотношений могут служить правила вычисления членов арифметической прогрессии

an+1=an+d  ,   где  d - разность прогрессии,

либо геометрической прогрессии

an+1=q an  ,   где  q - коэффициент прогрессии.

Эта идея рекурсии реализована и в языке Pascal.

Определение 16.1. Функция (процедура) на языке Pascal называется рекурсивной, если в ходе своего выполнения она обращается к самой себе.

Например, мы можем определить вычисление функции n!
рекурсивно. Как это сделать, показано на рисунке 16.1

function  Factorial (n : integer) : integer ;

begin   if  n>0  then Factorial:=Factorial (n-1)*n

                      else  if n=0 then Factorial:=1

                                      else writeln (’значение n меньше 0’)

end {Factorial}

Рис. 16.1. Функция вычисления n! в рекурсивной форме.

Рассмотрим подробно, как будет выполняться обращение к этой функции, напрмер, при n=4.

На рисунке 16.2 показан процесс вычисления для случая Factorial(4).

		24

Рис. 16.2. Вычисление функции Factorial(n) для n=4.

Сначала образуется так называемый рекурсивный фрейм №1 при n=4. Для этого фрейма отводится память и в нем фиксируются все значения переменных тела функции при n=4. Отметим, что в рекурсивном фрейме фиксируются значения всех переменных функции, кроме глобальных.

   Затем происходит вызов Factorial(n) при n=3. Образуется фрейм №2, где фиксируются значения переменных тела функции при n=3. При этом фрейм №1 также хранится в памяти. Из фрейма №2 происходит обращение к Factorial(n) при n=2. В результате этого обращения образуется фрейм №3, где фиксируются значения переменных тела функции при n=2 и т.д. до тех пор, пока при очередном обращении к функции Factorial условие n>0 не примет значение false.

   Это произойдет в фрейме №5. В этом фрейме мы получим значение Factorial =1 и передадим это значение в фрейм №4. После этого фрейм №5 будет уничтожен, так как обращение Factorial(n) при n=0 будет выполнено.

   В фрейме №4 мы вычислим значение Factorial(n) для n=1. После чего мы передадим это значение во фрейм №3, а фрейм №4 будет закрыт, так как обращение к Factorial(n) при n=1 будет закончено.

   Так мы будем сворачивать эту цепочку фреймов в последовательности, обратной той, в которой мы их порождали, пока не свернем фрейм №1. После чего вычисление функции будет окончено.

   Рекурсия возможна не только в случае функций, но и процедур. Пример рекурсии для процедур приведен на рисунке 16.3. Там показано описание рекурсивной процедуры для распечатки (вывода на печать) строки символов в порядке, обратном их вводу.

Procedure  BackPrint ;

var   символ : char ;

begin read (символ) ;

        if  символ  = EOL {EOL - End Of Line - специальное значение типа

                                   СHAR, соответствующее окончанию ввода}

        then writeln (   ) ; {пред началом вывода надо убедиться, что

                                  печатать будем с новой строки}

        else  begin  BackPrint ; write (символ) end

end {Procedure}

Рис 16.3. Пример рекурсивной процедуры.

(Косвенная рекурсия.) Итерация и рекурсия.

   Нетрудно заметить сходство между циклическими конструкциями (повторениями) и рекурсией. На рисунке 16.4 показана схема цикла вида while do и его рекурсивного аналога.

Рис. 16.4. Схема организации цикла вида while do

и его рекурсивного эквивалента.

Обратите внимание, что в правой части рис. 16.4 возможно зацикливание! Надо быть очень осторожным и всякий раз, применяя рекурсивную поцедуру или функцию, убедиться в их корректном завершении. Рассмотрим пример. На рисунке 16.5 приведен алгоритм Евклида, с которым мы познакомились на лекции 1, для вычисления НОД (наибольшего общего делителя) в форме обычной и рекурсивной функции на языке Pascal.

Function НОД (a, b : integer) : integer ;

Рис. 16.5. Циклическая и рекурсивная функции

для вычисления НОД.

Как видно из приведенных примеров на рисунках 16.1 и 16.5, итерация, т.е. цикл всегда может быть заменен его рекурсивным аналогом по схеме, показанной на рисунке 16.4.

   С обратным утверждением о замене рекурсии итерацией все сложнее. На рисунке 16.6 приведен пример рекурсивной функции, где по схеме (рис. 16.4) рекурсию итерацией заменить не удается.

в остальных случаях

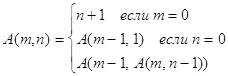
Рис. 16.6. Рекурсивная функция Аккермана.

Способы повторного использования процедур и функций.

Итак, процесс абстракции в форме процедуры состоит из трех шагов:

Именование. Присвоить рутинному алгоритму уникальное имя, которое затем будем использовать как имя соответствующей процедуры.

Определить пред- и постусловия для создаваемой процедуры или функции в соответствии с контекстом их использования в основной программе.

Параметризиовать процедуру. (Везде далее, если явно не оговорено, говоря о процедурах, будем иметь в виду также и функции). Для этого часть предусловия и постусловия в спецификации оформить в виде параметров соответствующего типа, часть из которых будет доставлять исходные данные, а другая часть - результаты работы процедуры.

Обобщить типы параметров. Проанализировать все места в программе, где будет обращение к данной процедуре на предмет, какие типы данных используются в этих местах, как они соотносятся с типами параметров в процедуре. Назовем совокупность типов данных в месте вызова процедуры контекстом обращения к процедуре Определить типы параметров так, чтобы они соответствовали как можно большему числу контекстов обращений к процедуре.

Реализовать получившуюся абстракцию рутинного алгоритма либо в форме процедуры, либо функции.

Мы не в праве ожидать, что выделенные нами уже существующие функции или процедуры, которые могут быть нам полезны для создания нашей новой программы, мы сможем использовать в том виде, как они есть. Есть четыре основных способа адаптации или повторного использования уже существующих рутинных алгоритмов и процедур для новых целей. Это - присоединение, вложение, настройка и слияние.

Присоединение. Этот способ предполагает, что если у нас есть процедура P1 c предусловием Q1  и постусловием R1 и процедура P2 c пред-и c постусловиями Q2  и R2 соответственно, (причем R1Þ Q2) , то мы можем построить процедуру P c предусловием Q1  и постусловием R2 последовательно соеденив Р1 и P2 так, как показано на рис.16.7.

P      {Q1}

{R1 Þ Q2}

{R2}

Рис. 16.7. Присоединение процедур Р1 и P2 .

Вложение. Этот способ применяется, когда новая процедура P образуется вложением известной процедуры P2 внутрь другой известной процедуры P1. Вложение возникает либо когда мы явно вставляем P2 как тело цикла или как альтернативу в теле процедуры P1 , либо когда P2 - это параметр для P1 .

Настройка. Суть этого способа состоит в том, что существующую процедуру Р1 мы либо обобщаем, либо, наоборот, сужаем в соответствии со спецификацией Р.

Например, если у нас есть процедура выбора максимального числа из массива из 100 натуральных чисел, то легко ее можем обобщить на случай массива из 1000 целочисленных компонентов.

Слияние. Этот способ построения новой процедуры Р за счет слияния, объединения двух существующих процедур Р1 и P2 .

Например, пусть процедура Р1 выбирает максимальное, а P2 - минимальное значения в массиве из 100 целых чисел. Тогда, объединив операторы процедуры Р1 и процедуры P2 в надлежащем порядке, мы получим процедуру Р , выбирающую max и min из 100 целых чисел.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.ergeal.ru/