Шумы определяют емкость канала и задают частоту ошибок при передаче цифровых данных. Шум по своей природе нестабилен и можно говорить лишь о том, что его величина с некоторой вероятностью лежит в определенном интервале значений. Плотность вероятности p(x) определяет вероятность того, что случайный сигнал X имеет значение амплитуды в интервале между x и x+Dx. При этом вероятность того, что значение х лежит в интервале между x1 и x2 определяется равенством:

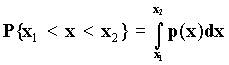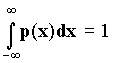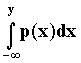, условием нормировки при этом является равенство . P(x) ероятность, а p(x) лотность вероятности. Вероятность того, что x меньше некоторой величины y равна , откуда следует, что P{x1 <>2} = P(x2) x1}, а

Так называемый белый шум подчиняется непрерывному нормальному (Гауссову) распределению 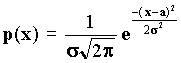, где а реднее значение x, а s реднеквадратичное отклонение х от a. В случае шумов среднее значение х с учетом полярности часто принимает нулевое значение (а=0).

В этом случае, если мы хотим знать вероятность того, что амплитуда шумового сигнала лежит в пределах ± v, то можно воспользоваться выражением

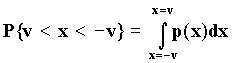
Для вычисления P{x1<x<-x1} обычно используются равенства
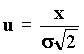и . Тогда P{x1<X<-X1} = = .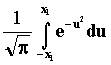

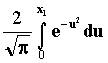Распределение P(x) обычно называется функцией ошибок (erf(x) = -erf(-x)). Полезной с практической точки зрения является вероятность

P{-ks<X<Ks}=Pk(k s) = 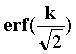, которая позволяет оценить возможность того, что шумовой сигнал превысит некоторый порог, заданный значением k.

Из числа дискретных распределений наиболее часто используемым является распределение Пуассона.
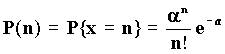, где n = 0, 1, 2, +; a=mP, m исло испытаний. Распределение Пуассона описывает вероятность процессов, где P<<1. При большом значении m отношение n/m приближается к значению вероятности P.
Среднее значение x 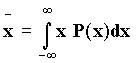, а для дискретного распределения 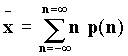. Среднеквадратичное отклонение s случайной величины х определяется как: 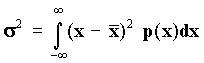, то же для дискретного распределения .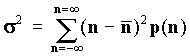

Как уже говорилось, во многих случаях шум имеет гауссово распределение с нулевым средним значением амплитуды. В этих случаях среднее значение мощности шумового сигнала равно вариации функции плотности вероятности. В этом случае отношение сигнал-шум будет равно

. Если шум носит чисто тепловой характер, то s2=kTB. В общем случае s2 = EnB [Вт], где полоса B измеряется в Гц, En энергия шума.